By the end of the lesson, the learner should be able:
- to identify integers in different situations;
- to represent integers on a number line.
Activities
Activity 1
- Mark a reference point on a level ground.
- Make five steps from the reference point, marking each step.
- From the same reference point, make and mark five steps in the opposite direction.
- Using (0) as the reference point, assign a positive sign (+ve) to each of the number of steps made forward and negative sign (–ve) to each of the number of steps made backward.
- Discuss and share your work with other groups.
Note:
Consider moving forward as a positive direction whereas moving backward as a negative direction.
Activity 2
- Choose a reference point (O) on a level ground.
- Write numbers on cards to represent positive steps or negative steps.
- In groups, pick a card and make steps from the reference point according to the number of steps indicated.
Learning Point
Positive whole numbers, negative whole numbers and zero are called integers.
Activity 3
Consider the following integers:
–5, –1, +4, –3, 0, +1, +3, +2, +5, –4, –2
- Represent the integers on a number line.
- Discuss and share with other groups.
Learning Point
- All integers to the left of zero are negative while the ones to the right of zero are positive.
- On a number line, an integer is less than all other integers to the right of it and greater than all those to the left of it.
Example 1
Use greater than (>) and less than (<) signs to compare the following integers:
- (–2) and (+2)
- (–1) and (–7)
- (+3) and (–4)
Solution
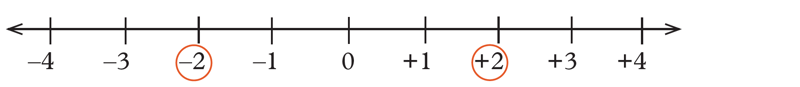
(–2) is on the left of (+2)
(–2) is less than (+2)
- (–2) < (+2)
(–7) is to the left of (–1)
(–7) is less than (–1)
- (–7) < (–1)
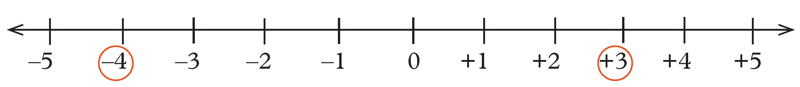
(+3) is on the right of (–4)
(+3) is greater than (–4)
- (+3) > (–4)
Exercise 1
Use a number line in the exercise.
Exercise 1.1
Identify the greater number in each pair on a number line.
- Greater is
-
(+3)
-
(–3)
- Greater is
-
(+5)
-
(+11)
- Greater is
-
(–11)
-
(+2)
Exercise 1.2
Identify the smaller number in each pair on a number line.
- Smaller is
-
(–8)
-
(–2)
- Smaller is
-
(–9)
-
(+4)
- Smaller is
-
(–1)
-
(+1)
Exercise 1.3
Use < or > signs to compare the following pairs of integers:
- (–4) (–7)
- (+2) (–9)
- (+3) (+5)
- (+8) (–8)
- (–5) (+2)
- (–12) (–15)
Exercise 1.4
Arrange the following integers from the smallest to the largest:
-
(–4)
-
(+1)
-
(–3)
-
(–7)
-
(–1)
-
(+5)
-
(+6)
-
(–2)
-
(+2)
-
(–3)
-
(–5)
-
(+8)
-
(–2)
-
(+9)
-
(–7)
-
(–9)
-
(+7)
-
(+3)
Expression
$$+
$$−
$$×
$$÷
$$
$$√
$$√
$$x
$$x
$$∞
$$;
$$(
$$)
$$[
$$]
$$=
$$≠
$$≤
$$≥
$$<
$$>
$$≈
$$≡
$$||
$$±
$$∓
$$x
$$%
$$€
- Service provided by Star Cloud Ltd